Ondas Estacionarias
A seguir, apresentamos um breve estudo sobre o rendimento percentual de uma antena em relação à sua R.O.E.
Como veremos abaixo, quando um medidor de R.O.E. indicar uma leitura de 1,50 : 1 (Leia-se: um e meio, por um - ou, um vírgula cinqüenta por um), a eficiência ou o rendimento da antena será de 85% e a sua impedânciaestará com 78 ou 35 Ohms.
As antenas poderão ser de 52 ou 75 Ohms. Os instrumentos medidores da ROE são, normalmente, fabricados para 50/52 Ohms, porém, se for utilizado para antenas de 75 Ohms será detectada uma leitura pouco superior.
Por exemplo: Com um medidor de 52 Ohms detectar numa antena de 52 Ohms uma leitura de 1,25:1, em outra antena de 75 Ohms ele irá registrar, aproximadamente, 1,70:1 devido o descasamento da impedância entre o aparelho medidor e a referida antena de 75 Ohms. Neste exemplo específico, pode-se considerar 1,50:1 como leitura correta.
A redução das ondas estacionárias para níveis ideais nas freqüências centrais de trabalho podem ser conseguidas por meios práticos, tais como:
01- 01- Corte do cabo coaxial de interligação entre o transmissor e o sistema irradiante dentro do comprimento elétrico determinado pela freqüência central de trabalho.
Este cálculo é feito com as seguintes fórmulas:
a) Para antenas de Onda Completa L = 300 . 0,66 : F(MHz) = ...metros
b) Para antenas de 1/2 onda, dividir o resultado encontrado acima por 2 (dois) e, para 1/4 de onda dividir o resultado da fórmula de onda completa por 4 (quatro).
Para antenas Dipolos e Yagis usar o valor de 1/4 de onda multiplicado por um número ímpar cujo resultado seja compatível com o comprimento físico necessário à interligação transceptor/antena.
Para antenas Cúbicas de quadro; Delta Loop, etc. usar um seguimento de 1/4 de onda em cabo de 75 Ohms e o restante para interligar o transceptor à antena, o valor de 1/4 de onda multiplicado por um númeropar até completar o comprimento físico necessário à interligação desejada.
Para se calibrar antenas em 50 ou 52 Ohms, antes de se instalar na torre ou no mastro de difícil manuseio é aconselhável utilizar, ainda a uma altura de 1,50 m de sólo, um cabo de 1/2 onda (L= 300 . 0,66 : 2 = ...metros), o F (MHz) qual, deverá ser ligado diretamente ao transmissor e, no seu extremo, um medidor de ROE e, em seguida a antena a ser sintonizada.
Desta forma ajustada, a antena a ser colocada na torre já subirá com a impedância correta e se tiver que ser calibrada, será pelo cabo coaxial de alimentação entre ela e o rádio transmissor. Se o cabo definitivo de interligação estiver com sua impedância correta de 50/52 Ohms o casamento será perfeito e não necessitará de outros ajustes. Usar sempre Cabos Coaxiais de boa procedência e que tenha garantia de uma impedância de 50 ou 52 Ohms.
02 - Afastar o máximo possível a antena de partes metálicas; paredes; árvores; redes elétricas; telhados; lajes de concreto armado; "estais" de material condutor; etc.
03 - Aumentar o máximo possível, a altura da antena do solo ou telhados; lajes de concreto armado, etc., melhorando sue plano refletor inferior. (terra).
04 - Alongamento ou encurtamento do comprimento dos elementos irradiantes (se for (dipolos) e, também, proporcionalmente, os elementos parasitas, se for Yagis.
L = 142,65 = ..... metros.
F(MHz) Como o próprio nome diz, uma antena de 1/2 onda é formada por 2 (dois) seguimentos de 1/4 de onda, cada. Logo, o valor encontrado na fórmula acima deve ser dividido por 2 para acharmos o comprimento de cada secção de 1/4 de onda que formará a 1/2 onda desejada.
Exemplo: Calcular um dipolo de 1/2 onda para operar em 20 Metros Freqüência de 14,150 MHz.
Temos: 142,65 : 14,150 = 10,08 m. Cada seguimento do dipolo terá: 10,08 : 2 = 5,04m. para cada lado. Notar que, nestes cálculos, consideramos as perdas de 5% (cinco por cento) em relação ao cálculo básico do comprimento original de uma onda elétrica completa que é:
L' = 300 : F(MHz) = ... m,
1/2 onda original seria:
L² =150 : F(MHz) =...m
1/4 de onda original seria:
L³ = 75:F(MHz)=...m
(As fórmulas L'; L² e L³ acima não devem ser usadas diretamente para os cálculos de dipolos irradiantes pois não contemplam as perdas de 5% originárias da resistência à passagem da corrente elétrica nos materiais condutores e irradiantes.
Para utilizá-las nos cálculos dos dipolos deve-se multiplicar o resultado encontrado por 0,95 o que reflete numa redução do valor encontrado em 5%).
|
R O E DA ANTENA
|
Rendimento da Antena
|
IMPEDÂNCIA DA ANTENA EM OHMS
|
CONCLUSÃO
|
|
* 1,00 : 1
|
100%
|
52 OU 50
|
IDEAL
|
|
1,05 : 1 1,10 : 1 1,15 : 1 1,25 : 1 1,30 : 1
|
99,00% 98,00% 96,00% 95,00% 94,00%
|
54 OU 49 57 OU 47 60 OU 45 63 OU 43 66 OU 40
|
ÓTIMO
|
|
1,35 : 1 1,40 : 1 * 1,50 : 1 1,55 : 1
|
90,00% 86,00% 85,00% 84,00%
|
70 OU 38 73 OU 37 78 OU 35 81 OU 33
|
ACEITÁVEL
|
|
1,65 : 1 1,75 : 1 1,85 : 1 1,95 : 1
|
80,00% 78,00% 76,00% 74,00%
|
87 OU 31 90 OU 30 96 OU 28 100 OU 27
|
RUÍM
|
|
2,10 : 1 2,15 : 1 2,30 : 1 2,60 : 1 3,00 : 1
|
70,00% 68,00% 60,00% 50,00% 40,00%
|
109 OU 25 113 OU 24 120 OU 23 135 OU 20 156 OU 18
|
PÉSSIMO
|
FONTE : INCTEST / IND. BRASILEIRA.
SALVADOR - BAHIA, 24/04/06
COLABORAÇÃO/DIVULGAÇÃO: PY6LA - Lima
As ondas estacionárias são importantes tanto em sistemas eletrônicos como mecânicos. Assim, seu conhecimento é de grande importância para a realização de projetos mecatrônicos e de radiotransmissão. Na verdade a maioria dos leitores que já montou um transmissor já ouviu falar das ondas estacionárias. Estas ondas, que aparecem nas linhas de transmissão devem ser mantidas num nível baixo para que o rendimento das emissões e dos próprios equipamentos não sejam comprometidos. Mas, o que são realmente estas ondas, como se formam e como pode ser reduzida sua ação e, finalmente como podem ser medidas é algo que não são muitos os que conhecem a ponto de poder tomar decisões em sua função. Tudo isso é o que veremos neste artigo.
Para que um transmissor funcione corretamente, toda energia de alta freqüência gerada nos circuitos eletrônicos deve ser leveda à antena e irradiada.
Para esta finalidade existe um elemento físico, um cabo denominado "linha de transmissão" que faz a conexão dos dois: transmissor à antena, conforme mostra a figura 1.
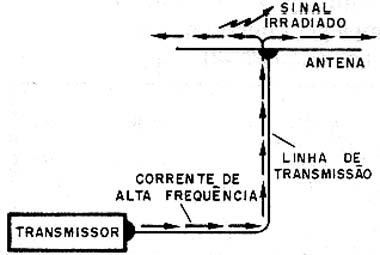
Essa linha não apresentaria interesse maior para os operadores ou projetistas das estações de rádio se não fosse alvo da ocorrência de um fenômeno importante, capaz de reduzir consideravelmente a eficiência do sistema.
Se ocorrerem problemas de adaptação entre a linha e o transmissor ou entre a linha e a antena, ocorrem sérios problemas na transferência da energia.
Reflexões podem então reduzir a energia irradiada e não é só isso: essa energia não transmitida volta para os circuitos do transmissor podendo sobrecarregá-los a ponto de causar a queima de componentes importantes.
Os sinais que refletem na linha de transmissão dão origem às chamadas "ondas estacionárias", ou do inglês "standing waves".
Estas ondas que também se manifestam em sistemas mecânicos como por exemplo uma onda que se propaga através de uma corda vibrante é o assunto que passamos a abordar em maior profundidade.
Até mesmo com ondas sonoras que se propagem num tubo o fenômeno pode ocorrer com grande intensidade com efeitos bastante interessantes que merecem ser conhecidos de nossos leitores.
Estes efeitos podem ser usados em sistemas de detecção de objetos com a medida da distância (trenas) em robôs e outros dispositivos mecatrônicos.
TRANSFERÊNCIA DE ENERGIA
Para que ocorra a máxima transferência de energia de um sistema para outro como, por exemplo, de um transmissor para uma antena, é preciso que suas impedâncias sejam iguais.
Se a ligação de um sistema A a um sistema B for direta conforme mostra a figura 2, o modo como esta ligação é feita não ‚ importante, pois os fios não influem na transferência da energia.
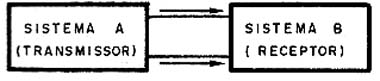
Entretanto, se o sistema A (um transmissor por exemplo) estiver longe do sistema B (uma antena, por exemplo) é preciso que o cabo que os une, ou seja, a linha de transmissão tenha características apropriadas, para que não ocorram modificações no processo.
A linha de transmissão deve ter a mesma impedância dos outros elementos do sistema, ou seja, o transmissor e a antena, conforme mostra a figura 3.
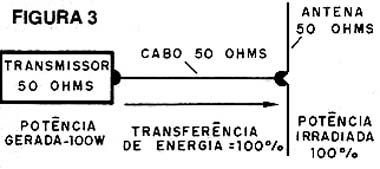
Para fios comuns, a impedância apresentada depende do comprimento considerado, o que não os torna muito próprios para serem usados na ligação de transmissores a uma antena.
Isso ocorre porque, em altas frequências, entram em ação a indutância dos fios e a capacitância entre eles, a qual depende justamente do comprimento, conforme mostra a figura 4.
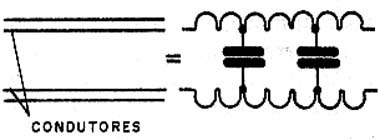
Para a condução de tais sinais existe; entretanto uma solução que consiste no uso de fios especiais, ou seja, cabos, em que a construção física é tal que a impedância, para uma ampla faixa de freqüências, se mantém constante independentemente do comprimento do fio e da própria freqüência do sinal que deve ser conduzido.
Assim, quando dizemos que um cabo coaxial tem uma impedância de 75 ohms ou 50 ohms, não importa se o comprimento considerado seja de 20 centímetros ou 20 metros.
Na figura 5 temos o modo como um cabo coaxial é construído, observando-se a blindagem externa e o condutor interno.
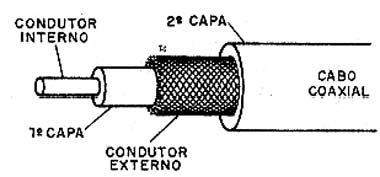
Com a utilização de um transmissor cuja saída seja de 50 ohms de impedância, de um cabo de 50 ohms de impedância (qualquer comprimento) e uma antena de 50 ohms, teríamos certamente o máximo rendimento para uma estação.
Na prática, entretanto, se podemos manter a impedância do transmissor no valor certo, do cabo no valor certo a da antena nem sempre se ajusta perfeitamente a isso e aí começam a aparecer os problemas.
IMPEDÂNCIA DE ANTENA
Para entender melhor fenômeno vamos imaginar um sistema em que tenhamos um transmissor, um cabo coaxial, mas em lugar da antena seja colocada uma lâmpada, conforme mostra a figura 6.
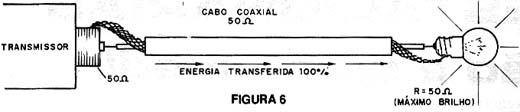
Vamos supor inicialmente que a lâmpada tenha uma resistência constante de filamento, igual a 50 ohms, e que corresponda à impedância da linha de transmissão e da própria saída do transmissor.
Ligando o transmissor, toda a energia ser transferida para a lâmpada que a absorverá e a converterá em luz e calor.
A lâmpada acenderá então com seu brilho normal.
Se em seu lugar for ligada uma antena de 50 ohms a transferência de energia para o espaço na forma de ondas eletromagnéticas será total.
O que aconteceria se em lugar de uma lâmpada de 50 ohms fosse ligada uma de 150 ohms, conforme mostra a figura 7?
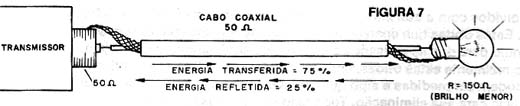
O resultado seria um "descasamento de impedâncias".
A lâmpada não conseguiria absorver toda a energia do transmissor vinda pelo cabo e não tendo o que fazer com o excedente dessa energia, ela a refletiria de volta ao transmissor.
A absorção seria de 75% e a parte refletida de 25%.
É claro que esta energia refletida terá de ir para algum lugar pois não pode ficar "acumulada" no fio, e este algum lugar são os componentes de saída do circuito do transmissor.
Estes componentes têm de dissipar esta energia refletida, transformando-a em calor, já que não ela pode ser irradiada, e o resultado será um aquecimento adicional que pode causar problemas de funcionamento.
Nem sempre o projeto prevê um aquecimento muito maior do que o obtido em funcionamento normal e isso pode causar a queima de componentes.
Para um transmissor transistorizado pode ocorrer a queima dos transistores de saída e para os transistores valvulados teremos um "avermelhamento" das placas das válvulas com uma sobrecarga e redução da vida útil.
Por que a onda refletida faz tudo isso? O que ocorre dentro do cabo?
Para entender estes fatos vamos um pouco além nas nossas explicações tomando uma
analogia mecânica.
Na verdade esta analogia mecânica se aplica aos sistemas que podem estar num dispositivo que transfira energia através de uma corda, de um tubo usando algum tipo de vibração mecânica.
AS ONDAS ESTACIONÁRIAS
Imaginemos uma corda com uma extremidade presa a uma parede, conforme mostra a figura 8.
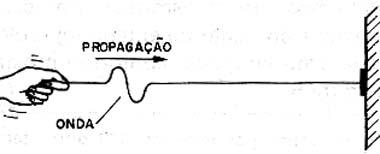
Movimentando rapidamente para cima e para baixo a extremidade livre da corda, podemos produzir uma onda transversal que se propaga com uma certa velocidade.
O comportamento desta onda é análogo ao de uma onda elétrica que percorre um cabo coaxial.
A única diferença é que no caso do sinal elétrico temos uma tensão que varia ao longo da linha e a percorre numa velocidade de centenas de milhares de quilômetros por segundo.
No cabo temos uma amplitude mecânica e a velocidade de propagação é da ordem de centenas de metros por segundo, conforme o material de que ele é feito.
Pois bem, se na extremidade fixa da corda houver um sistema de amortecimento que possa absorver toda a energia que é transportada pela onda transversal tudo bem: a onda chega a este ponto e transfere sua energia desaparecendo.
No entanto, se esta oscilação não tiver sua energia absorvida, a onda reflete e volta ao ponto de partida, conforme mostra a figura 9.

Temos então uma onda refletida que pode ter maior ou menor intensidade, conforme a energia que eventualmente tenha sido absorvida no ponto fixo de reflexão.
No caso de um transmissor de rádio não temos simplesmente uma onda mas sim a produção constante de ondas, ou um trem de ondas, e essas ondas vão continuamente do transmissor para a antena.
Seria como o movimento constante da mão (transmissor) produzindo as ondas que vão para a antena parede, conforme mostra a figura 10.
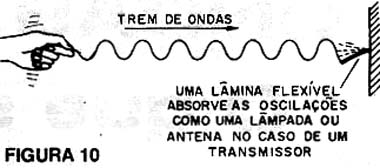
Isso significa que, se houver reflexão dessas ondas no final da linha, as ondas que vão se combinam com as ondas que vem e o resultado é bastante interessante: como as freqüências das ondas num sentido e noutro são iguais (seus comprimentos também), ocorre um fenômeno de batimento em que aparecem pontos de máximos e mínimos fixos, bem estabelecidos ao longo da extensão da linha ou corda, conforme mostra a figura 11.
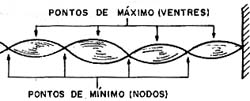
Se a intensidade da onda refletida for a mesma da onda incidente, ou seja, se tivermos 100% de reflexão, os pontos de máximo terão a intensidade (amplitude) correspondente ao dobro da amplitude de cada sinal e os pontos de mínimo corresponderão a nulos.
Se a intensidade da onda refletida for menor, os máximos não terão o dobro da amplitude do sinal original e os mínimos não serão nulos.
A diferença entre elas será menor e teremos uma forma de oscilação conforme mostrada na figura 12.
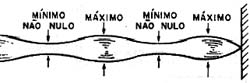
Levando isso para o caso eletrônico, tomando um transmissor como fonte de sinais, podemos imaginar voltímetros ao longo da linha de transmissão, conforme mostra a figura 13.
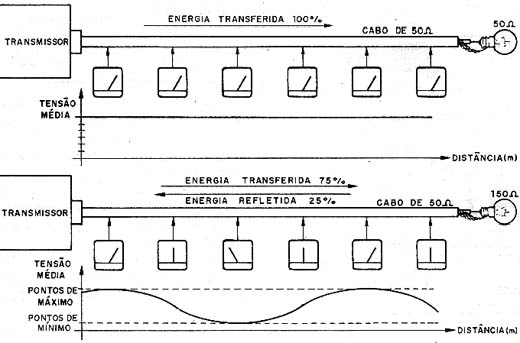
Se não houver reflexão alguma dos sinais, a tensão marcada em qualquer voltímetro será máxima, qualquer que seja o ponto da linha em que ele seja ligado.
Por outro lado, se o sinal refletir totalmente no final da linha, teremos pontos fixos em que os voltímetros indicarão máximos e pontos que indicarão nulos.
Veja que, observando essas indicações e mesmo a oscilação da corda, temos a impressão que a onda "pára", ou seja, passamos a ter nós e ventres em posições fixas.
Na realidade existe uma propagação de ondas nos dois sentidos, resultando no fenômeno, mas sua combinação leva à impressão de uma só que esteja estacionada ou estacionária, daí darmos ao fenômeno o nome de "ondas estacionárias".
Para a transmissão, a presença de ondas estacionárias é sinal de que existe energia sendo refletida e portanto não irradiada.
Devemos portanto reduzir sua proporção no sentido de obter maior rendimento na transferência dos sinais.
COMO MEDIR
Em princípio sabemos que, para que haja total transferência de energia do transmissor para a antena, não devemos ter nenhum sinal refletido.
Em outras palavras, em todos os pontos considerados da linha de transmissão a tensão deve ser a mesma.
A relação entre as intensidades observadas entre os pontos de máximos e de mínimos é de 1:1 (um para um).
Obtemos então o maior rendimento de um transmissor quando a relação de ondas estacionárias observadas no sistema for de 1 para 1.
Esta relação de ondas estacionárias é abreviada por ROE.
Nos livros técnicos que mantém os termos em inglês a abreviação é SWR (Stand Wave Ratio).
À medida que aparecem as ondas estacionárias em conseqüência da reflexão do sinal, a relação entre a tensão nos pontos de máximos e mínimos de sinal aumenta.
Damos como exemplo uma tabela em que associamos as relações de ondas estacionárias (ROE) à potência perdida.
R.O.E. Perda (%)
1 : 1,01 -
1 : 1,02 0,01
1 : 1,03 0,02
1 : 1,04 0,04
1 : 1,05 0,06
1 : 1,06 0,08
1 : 1,07 0,11
1 : 1,08 0,15
1 : 1,09 0,19
1 : 1,10 0,23
1 : 1,11 0,27
1 : 1,12 0,32
1 : 1,13 0,37
1 : 1,14 0,43
1 : 1,15 0,49
1 : 1,16 0,55
1 : 1,17 0,61
1 : 1,18 0,68
1 : 1,19 0,75
1 : 1,20 0,83
1 : 1,30 1,70
1 : 1,40 2,78
1 : 1,50 4,00
1 : 1,60 5,33
1 : 1,70 6,72
1 : 1,80 8,16
1 : 1,90 9,63
1 : 2,00 11,1
1 : 2,20 14,1
1 : 2,40 17,0
1 : 2,60 19,8
1 : 2,80 22,4
1 : 3,00 25,0
1 : 4,00 36,0
1 : 5,00 44,4
1 : 6,00 51,0
1 : 7,00 56,0
1 : 8,00 60,5
1 : 9,00 63,2
1 : 10 66,9
1 : 20 81,9
1 : 50 92,3
Evidentemente, um medidor de ondas estacionárias deve ter condições de captar tanto o sinal que vai do transmissor como o que é refletido da antena para o receptor, diferenciando-os de modo a se obter a indicação desejada.
Para conseguir isso os circuitos usam recursos interessantes.
O ACOPLADOR DIRECIONAL
Uma das características de uma linha de transmissão é que o campo externo é nulo de modo que não podemos extrair nenhum sinal em suas proximidades, do lado externo.
É justamente esta propriedade que permite a constância de sua impedância, independendo de seu comprimento.
Se quisermos extrair parte do sinal de um cabo coaxial por indução, precisamos passar um condutor sob sua malha, fazendo-o correr paralelo ao condutor interno conforme mostra a figura 14.
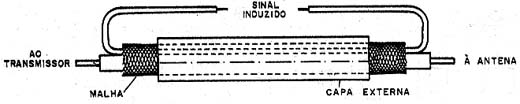
Nestas condições, teremos nas extremidades deste condutor uma tensão que depende em valor e freqüência do sinal que está sendo transmitido.
Partindo desta configuração, podemos ir um pouco além e colocar um diodo e um instrumento, conforme mostra a figura 15.
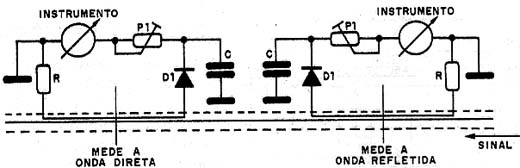
A polarização do diodo é tal que permite que apenas os sinais que correm num sentido sejam medidos.
O que ocorre é que, cortando parte dos semiciclos que correspondem à reflexão ou à incidência dos sinais, podemos ter uma indicação ou do sinal direto ou do sinal refletido.
Veja então que aproveitando este tipo de acoplamento direcional podemos facilmente saber qual é a "quantidade" de sinal refletido e com isso saber qual é a relação de ondas estacionárias.
Bastar ligar o acoplador de modo a medir as ondas "diretas" e depois inverter a ligação para ler as ondas "refletidas" e estabelecer a relação.
Isso nos leva então à configuração final de um instrumento para esta finalidade que é mostrado na figura 16.
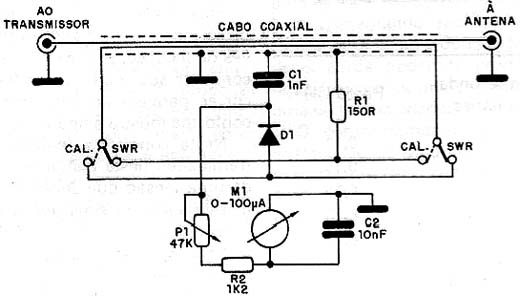
Sua operação é muito simples: colocando a chave leitora na posição de ajuste, medimos o sinal no sentido direto (transmissor para a antena) e com isso podemos fazer o ajuste para que o valor indicado seja 100% ou 1.
Depois, invertendo a posição da chave, medimos o sinal refletido, obtendo deste modo uma indicação direta da relação de ondas estacionárias ou da porcentagem de sinal transferido.
Veja que esta necessidade de termos de ajustar o instrumento para o fim da escala na condição de sinal direto faz com que a sensibilidade do instrumento determine a potência mínima que o transmissor deve ter para a sua utilização.
Os instrumentos deste tipo são então especificados para potências mínimas em que operam e também, para uma determinada faixa de freqüências.
Como a tensão induzida no fio interno ao cabo coaxial depende também da potência, podemos usar o mesmo instrumento como indicador de potência.
Basta então ter uma referência na escala obtida por calibração para que, na posição de sinal direto, tenhamos a possibilidade de medir diretamente a potência do transmissor.
MEDIDORES DE ONDA ESTACIONÁRIA COMERCIAIS
Comercialmente o medidor de onda estacionária pode ser adquirido para operar com transmissores, principalmente da faixa de radioamadores (PX e PY), se bem que existam os tipos profissionais que são indicados para operação em diversas faixas de telecomunicações, incluindo freqüências da faixa de VHF, UHF e SHF.
Estes aparelhos, como o mostrado na figura 17 são bastante simples e sua precisão é suficientemente boa para permitir que os operadores levem seus equipamentos de transmissão à condição de máximo rendimento.

Figura 17 - Um medidor de ROE (SWR)
Os medidores de ondas estacionárias são intercalados entre o transmissor e a antena, conforme mostra a figura 18.
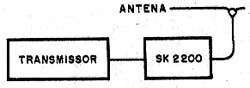
Como todo instrumento de medida deste tipo (sem sistema ativo), a energia que aciona o instrumento indicador é tirada do próprio circuito, o que significa uma pequena atenuação do sinal.
Neste caso, a atenuação é de apenas 0,5% o que significa uma boa precisão para as medidas, mesmo de transmissores de pequena potência.
COMO MEDIR
A operação dos medidores é feita de maneira semelhante na maioria dos tipos.
Assim para que o leitor tenha uma idéia de como isso pode ser feito, vamos dar como exemplo a operação de um medidor típico como o tomado como exemplo no item anterior.
a) Medindo potência (PWR)
Inicialmente a chave seletora do instrumento deve ser ajustada para medir potência, ou seja, colocada na posição PWR.
Depois, ajusta-se o potenciômetro de Calibração para a freqüência de transmissão, de acordo com a tabela fornecida pelo fabricante do instrumento.
A seguir, acionando-se o transmissor de modo que ele transmita seus sinais, faz-se a leitura do valor da potência diretamente na escala correspondente do instrumento.
b) Medindo ondas estacionárias (SWR)
Inicialmente, coloque a chave seletora na posição que mede as ondas diretas (SWR-FWD).
Ajuste então o potenciômetro de calibração até obter a indicação de máximo ou ainda o ponto indicado por SET pelo fabricante.
Este ajuste deve ser feito com o transmissor ligado.
Passe agora a chave seletora para a posição que mede a onda refletida (SWR).
Basta então ler a porcentagem de onda refletida ou ainda a relação de ondas estacionárias (SWR ou ROE) diretamente na escala correspondente.
Ao fazer a medida deve ser observado o mínimo de potência do transmissor para a freqüência correspondente de modo a se conseguir o ajuste do aparelho.
Fonte Instituto Newton C. Braga
www.newtoncbraga.com.br/index.php/telecom-artigos/1713-tel010.html
